Arithmatic (अङ्कगणित)
(Tax, Money Exchange, Compound Interest, Population Growth & Price Depreciation)
1. Tax (कर)
1.1. मुल्य अभिवृद्धि कर -मु.अ.क. (Value Added Tax - VAT)
मूल्य अभिवृद्धि कर बिक्रिका प्रत्येक चरणमा बढेकाे मूल्यमा लाग्ने कर हाे । अर्काे शब्दमा, मूल्य अभिवृद्धि कर त्यस्ताे कर हाे जुन उत्पादन देखि खुद्रास्तरसम्म हरेक तहकाे मूल्य वृद्धिमा वस्तु तथा सेवा दुवैमा लगाइन्छ ।
(Value added tax is a multistage tax which is levied on increased price in distribution (supply) channels. In other words, value added tax (VAT) is a tax on goods and services (except export and government service) it falls on the value added of each stage from the stage of production to rtail stage.)
1.2. महत्वपूर्ण सुत्रहरु (Important Formullas)
🚀 $\large \textbf{Example: 1.}$ रु. 2,700 मा 13% मूल्य अभिवृद्धि कर जाेड्दा आउने मुल्य रु.3,060 भन्दा कतिले कम छ?
How much is less the value including 13% vat on Rs.2,700 than Rs.3,060?
Here,
$ \text{$1^{st}$ price = Rs.2700}$
vat =13 %
$2^{nd}$ price= Rs.3060
Now, $1^{st}$ price including vat = Rs.2700 + Rs.2700 of 13 %
or, $1^{st}$ price including vat = $Rs.2700+Rs.2700 \times \frac{13}{100}$
or, $1^{st}$ price including vat = $Rs.2700+Rs.27 \times 13 \Longrightarrow \text{calceling 00}$
or, $1^{st}$ price including vat = Rs.2700+Rs.351
or, $1^{st}$ price including vat = Rs.3051
Hence, $1^{st}$ price including vat is (3060-3051=) Rs.9 less than $2^{nd}$ price.
$\large \textbf{Example: 2.}$
एउटा वस्तुकाे 13 % मुल्य अभिवृद्धि करसहितकाे मूल्य रु.5763 छ भने मूल्य अभिवृद्धि कर रकम कति हाेला?
The Price of an object with 13% VAT is Rs.5763. What will be the value added tax amount?
Here,
$ vat = 13 \% $
मुल्य अभिवृद्धि करबाहेककाे मूल्य (CP)= x (say)
मुल्य अभिवृद्धि करसहितकाे मूल्य (SP)= रु.5763
मुल्य अभिवृद्धि कर रकम (vat Amount) = ?
By the formula, $SP = \frac{CP(100+vat \%)}{100}\\
or, 5763 = \frac{x(100+13)}{100}\\
or, 5763 \times 100 = x(113) \Longrightarrow \text{cross multiply}\\
or, \frac{576300}{113} = x \Longrightarrow \text{dividing both side by 113}\\
\therefore x =Rs. 5100 $
Then, भ्याट रकम (Vat Amount) = Rs.5100 of 13% = $5100 \times \frac{13}{100}$=Rs.663.
एउटा रेडियाेकाे अङ्कित मूल्य रु.5000 राखिएकाे थियाे, साे रेडियाेमा 15% छुट दिई 10% भ्याट लगाउँदा साेकाे मूल्य कति पुग्याे ?
The marked price of a radio was Rs.5000. What will be the price of the radio if 10% Vat was levied, after allowing 15% discount on it ?
Here,
अङ्कित मूल्य $(MP) = Rs. 5000\\
Vat = 10 \% $
छुट प्रतिशत $(D \%) = 15 \% $
बिक्रय मूल्य $(SP) = ? $
By the formula, $ SP = \frac{MP(100-D \%)(100+Vat \%)}{100 \times 100}\\
or, SP = \frac{5000(100-15)(100+10)}{100 \times 100}\\
or, SP = \frac{5000 \times 85 \times 110}{10000}\\
or, SP = \frac{46750000}{10000}\\
\therefore SP = Rs.4675
$
2. मुद्रा विनिमय (Money Exchange)
एउटा देशकाे मुद्रा लिएर वा दिएर साे रकम बराबरकाे अर्काे देशकाे मुद्रा दिने वा लिने प्रक्रियालाई मुद्रा विनिमय भनिन्छ ।
(Giving or Recieving of sum of money of one country equal in the value to a given sume of the currency of another country is known as Money Exchange)
2.1. खरिदर र बिक्रिदर (Buying Rate and Selling Rate)
बैंक वा बित्तिय संस्थाले विदेशी मुद्रा खरिद गर्दा दिने विनिमय दरलाई खरिदर र बिक्रि गर्दा दिने विनिमय दरलाई बिक्रि दर भनिन्छ । (The exchange rate which is given by bank or financial institute to buy foreign money is buying rate and the rate which is given to sell the foreign money is called the selling rate.)
2.1. Chain Rule (शृङ्खला नियम)
Rule (नियम)
1 अमेरिकी डलरकाे रु.70 काे दरले रु.50540 काे कति डलर हुन्छ?
Using the rate of Rs.70 for 1 US dollor, calculate the US dollars for Rs.50540.
Here,
1 US dollar = Rs.70
Rs.50540 = x Us dollar (say)
Using Chain Rule, $ 1 \times 50540 = 70 \times x \\
or, 50540 =70x \\
or, x = \frac{50540}{70} \\
\therefore x = 722 \text{US dollor. Ans.}$
एक जना व्यापारीले £1 = रु.140 काे दरमा रु.8,40,000 काे पाउण्ड स्टर्लिङ साट्याे । एकदिन पछि नेपाली मुद्रा 5% ले अधिमूल्यन भयाे र उक्त दिनमा उसँग भएकाे पाउण्ड पुनः नेपाली मुद्रामा साट्दा उसलाई कति नाफा वा नाेक्सान भयाे हाेला?
Abusiness man exchange Rs.8,40,000 into pound sterling at the rate of £1 = Rs.140. After one day, Nepali currency is revaluated by 5% and he exchanged the pounds which he had into Nepali currency again. What is his gain or loss ?
Here,
First condition:
£1 = Rs.140
Rs.840000 = £ x (say)
Using chain Rule, $ 1 \times 840000 = 140 \times x \\
or, 840000 = 140x \\
or, x = \frac{840000}{140} \\
\therefore x= £6000. \text{Ans.}$
Second Condition:
एकदिन पछि नेपाली मुद्रा 5% ले अधिमूल्यन भयाे । (After one day, Nepali Currency is revaluated by 5%.)
Then, £1 = Rs.140 - 5% of Rs.140. =Rs.140 - 140 $ \times \frac{5}{100}$= Rs.140 - Rs.7=Rs.133
Now, $£1 = Rs.133 \\
Rs. y \space (say) = £6000 \\$
Using Chain Rule, $ 1 \times y = 133 \times 6000 \\
\therefore y = Rs.798000 $
Hence, नाेक्सान (Loss) = Rs. 840000 - Rs.798000 = Rs.42000. ans.
3. चक्रिय ब्याज (Compound Interest)
3.1. परिचय (Introduction)
चक्रीय व्याज (Compound Interest) : कुनै मुलधन निश्चीत समय अवधि (वार्षिक वा अर्धवार्षिक) पश्चात व्याज गणना गरी व्याजालाई मुलधनमा जाेडेर पुनः व्याज निकालिन्छ भने त्यसलाई चक्रीय व्याज भनिन्छ । (Compound Interest is the interest which is calculated by adding the interest to the principal and calculating the interest at the end of a certain time.)
चक्रीय मिश्रधन (Compound Amount) : चक्रीय व्याज र मूलधनकाे याेगफललाई चक्रीय मिश्रधन भनिन्छ । (The sum of compound interest and principal is called Compound Amount)
वार्षिक चक्रीय ब्याज (Yearly Compound Interest) : कुनै मुलधन प्रत्येक वर्ष पश्चात ब्याज गणना गरी ब्याज निकालिन्छ भने त्यसलाई वार्षिक चक्रिय ब्याज भनिन्छ । (Yearly compound interest is the interest which is calculated by adding the interest to the principal and calculating the interest at the end of every year.)
अर्धवार्षिक चक्रीय ब्याज (Halp-yearly Compound Interest) : कुनै मुलधन प्रत्येक 6 महिना वा अर्ध वार्षिक पश्चात ब्याज गणना गरी ब्याज निकालिन्छ भने त्यसलाई वार्षिक चक्रिय ब्याज भनिन्छ । (Halp-yearly compound interest is the interest which is calculated by adding the interest to the principal and calculating the interest at the end of every six months.)
3.2. महत्वपूर्ण सुत्रहरु (Important Formullas)
समय (Time) = T, $\space $ वार्षिक ब्याजदर (Rate of Interest) = R, $\space$ साँवा (Principal) =T
चक्रीय मिश्रधन (Compound Amount) = CA
चक्रीय व्याज (Compound Interest) = CI
अर्धवार्षिक चक्रीय ब्याज (Halp-yearly Compound Interest) =HCI
अर्धवार्षिक चक्रीय मिश्रधन (Halp-yearly Compound Amount) =HCA
यदि T वर्ष र M महिना भएमाः
$\large \textbf{Example: 1.}$ बार्षिक 12% ब्याजदरमा रुपकले विदुरसँग रु.14000 कर्जा लिएछ भने 2 वर्षपछि विदुरलाई जम्मा कति चक्रीय ब्याज तिर्नुपर्ला ? सुत्र प्रयाेग नगरी हिसाब गर्नुहाेस् ।
Rupak borrowed Rs.14000 with Bidur at 12% annual rate of interest and how much compound interest should be paid by Rupak to Bidur? Calculate without using formula.
Here,
पहिलाे वर्षकाे लागि साँवा $(P_1)$ = Rs. 14000
पहिलाे वर्षकाे लागि ब्याजदर $(R)$ = 12%
पहिलाे वर्षकाे लागि समय $(T_1)$ = 1 year
पहिलाे वर्षकाे लागि साधारणा ब्याज $(SI_1) = \frac{P \times T \times R}{100} \\
=\frac{14000 \times 1 \times 12}{100} \\
=\frac{1680000}{100}\\
=Rs. 1680 $
दाेस्राे वर्षकाे लागि साँवा $(P_2)$ = Rs. 14000 + Rs. 1680=Rs.15680 ($P_2=P_1 +SI_1$)
दाेस्राे वर्षकाे लागि ब्याजदर $(R)$ = 12%
दाेस्राे वर्षकाे लागि समय $(T_2)$ = 1 year
दाेस्राे वर्षकाे लागि साधारणा ब्याज $(SI_1) = \frac{P \times T \times R}{100} \\
=\frac{15680 \times 1 \times 12}{100} \\
=\frac{188160}{100}\\
=Rs. 1881.6 $
अब, 2 बर्षपछिकाे वार्षिक चक्रिय ब्याज = $SI_1 + SI_2\\
=Rs. 1680 + Rs.1881.6 \\
=Rs. 3561.60 Ans.$
बार्षिक 21% ब्याजदरमा सन्ताेषले सुरेशसँग रु.130000 कर्जा लिएछ भने 2 वर्षकाे अन्तमा हुने साधारण ब्याज र बार्षिक चक्रीय ब्याज निकाल्नुहाेस् ।
Santosh borrowed Rs.130000 with Bidur at 21% annum. Find the simple interest at the end of 2 years and interest compounded yearly.
Here,
सावाँ (P) =Rs. 130000
ब्याजदर (R) = 21%
समय (T) = 2 years
साधारण ब्याज (SI) = ?
बार्षिक चक्रीय ब्याज (CI)= ?
By the formula, $SI=\frac{P \times T \times R}{100}\\
or, SI = \frac{130000 \times 2 \times 21}{100}\\
or, SI = \frac{5460000}{100} \\
\therefore SI = Rs.54600.$
Again, $CI = P[(1 + \frac{R}{100})^T - 1]\\
or, CI = 130000[(1 + \frac{21}{100})^2 - 1]\\
or, CI = 130000[(1 + 0.21)^2 -1]\\
or, CI = 130000[(1.21)^2 - 1]\\
or, CI = 130000[1.4641 - 1]\\
or, CI = 130000 \times 0.4641 \\
\therefore CI = Rs.60333. \space Ans.$
एउटा बैंकले खाता M मा 10% प्रतिवर्ष अर्धवार्षिक चक्रीय ब्याजदर र खाता N मा 15% प्रतिवर्ष चक्रीय ब्याजदर कायम गरेकाे छ। यदि तपाईं 2 वर्षका लागि रु.40,000 साे बैङ्कमा जम्मा गर्दै हुनुहुन्छ भने कुन खातामा जम्मा गर्नुहुन्छ र किन ? गणाना गरी कारणसहित उल्लेख गर्नुहाेस् ।
A bank has fixed the rate of interest 10% p.a. semi-annually compound interest in account M and 15% p.a annually compound interest in account N. If you are going to deposite Rs.40,000 for 2 years in the same bank, in which account will you diposit and why? Give your reason with calculation.
Here,
खाता M मा
अर्धवार्षिक चक्रीय ब्याजदर (R) = 10%
समय (T) = 2 years
सावाँ (P) = Rs.40,000
अर्धवार्षिक चक्रीय ब्याज (HCI) =?
By the formula, $HCI = P[(1 + \frac{R}{200})^{2T} - 1]\\
or, HCI = 40000[(1 + \frac{10}{200})^{2 \times 2} - 1]\\
or, HCI = 40000[(1 + 0.05)^4 - 1]\\
or, HCI = 40000[(1.05)^4 - 1]\\
or, HCI = 40000[1.2155 - 1]\\
or, HCI = 40000 \times 0.2155\\
\therefore HCI = Rs.8,620.$
खाता N मा
वार्षिक चक्रीय ब्याजदर (R) = 15%
समय (T) = 2 years
सावाँ (P) = Rs.40,000
वार्षिक चक्रीय ब्याज (CI) =?
By the formula, $CI = P[(1 + \frac{R}{100})^{T} - 1]\\
or, CI = 40000[(1 + \frac{15}{100})^{2} - 1]\\
or, CI = 40000[(1 + 0.15)^2 - 1]\\
or, CI = 40000[(1.15)^2 - 1]\\
or, CI = 40000[1.3225 - 1]\\
or, CI = 40000 \times 0.3225\\
\therefore CI = Rs.12,900.$
अतः म खाता N मा जम्मा गर्छु किनभने खाता N ले धेरै ब्याज दिनेरहेछ ।
4. जनसङ्ख्या वृद्धि र मिश्रह्रास (Population Growth and Price Depreciation)
4.1 जनसङ्ख्या वृद्धि (Population Growth)
सुरुकाे जनसङ्ख्या (Initial Population) = $P_0$
T वर्षपछिकाे जनसङ्ख्या (Popultion after T years) =$P_T$
जनसङ्ख्या वृद्धिदर (Population growth rate) =$R$
बढेकाे जनसङ्ख्या (Increased Population) =$P_G$
T वर्षकाे अन्त्यमा भएकाे मृत्यु सङ्ख्या =$D$
T वर्षपछि बसाइँसराइबाट प्रवेश भएकाे सङ्ख्या =$M_{in}$
T वर्षपछि बसाइँसराइबाट अन्यत्र गएकाे सङ्ख्या =$M_{out}$
4.2 मिश्रह्रास (Compound Depreciation)
सुरुकाे मूल्य (Initial Value) = $V_0$
T वर्षपछिकाे मूल्य (Value after T years) =$V_T$
ह्रासदर (depreciation Rate) =$R$
T वर्षपछि ह्रास भएकाे मूल्य =$V_{D}$
$\large \textbf{Example: 1.}$एउटा गाउँमा जनसङ्ख्या 20000 छ । यदि उक्त गाउँकाे जनसङ्ख्याकाे बृद्धिदर वार्षिक 2% भए 2 वर्षपछिकाे जनसङ्ख्या कति हाेला? पत्ता लगाउनुहाेस् ।
The population of the village is 20000. If the population growth rate of the village is 2% per annum, what will be the population after 2 years ? Find it.
Here,
सुरुकाे जनसङ्ख्या $(P_0)$ = 20000
वृद्धिदर (R) = 2%
समय (T) = 2 years
T वर्षपछिकाे जनसङ्ख्या $(P_T)$ = ?
By the formula, $P_T = P_0(1 + \frac{R}{100})^T \\
P_T = 20000(1 + \frac{2}{100})^2\\
P_T = 20000(1 + 0.02)^2\\
P_T = 20000(1.02)^2\\
P_T = 20000 \times 1.0404\\
\therefore P_T = 20,808 \space Ans.$
अतः २ वर्षपछिकाे जनसंख्या 20,808 हुन्छ ।
एउटा मेशिनकाे हालकाे मूल्य रु.650000 छ । प्रतिवर्ष 10% काे दरले मूल्य ह्रास कट्टा हुन्छ । 3 वर्षपछिकाे साे मेशिनकाे मूल्य कति हुन्छ ?
The current price of a machine is Rs.650000. If it is depreciated at the rate of 10%. What will be the value of the machine afeter 3 years ?
Here,
मेशिनकाे सुरुकाे मूल्य $(V_0)$ = 650000
ह्रासदर (R) = 10%
समय (T) = 3 years
T वर्षपछिकाे मूल्य $(V_T)$ = ?
By the formula, $V_T = V_0(1 - \frac{R}{100})^T \\
V_T = 650000(1 - \frac{10}{100})^3\\
V_T = 650000(1 - 0.1)^3\\
V_T = 650000(0.9)^3\\
V_T = 650000 \times 0.729\\
\therefore V_T = Rs.473850 \space Ans.$
अतः 3 वर्षपछि उक्त मेशिनकाे मूल्य Rs.4,73,850 हुन्छ ।






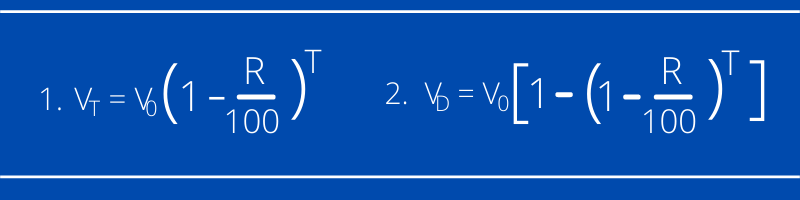









0 comments:
Post a Comment